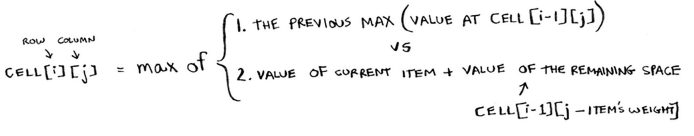Dynamic Programming
A technique used to solve problems by breaking them down into smaller subproblems and solving each subproblem only once, storing the results for future use. This avoids redundant calculations and makes the algorithm much faster compared to a naive recursive approach.
Example: Knapsack Problem
You have a knapsack that can hold 4 lbs. A shop offers the following items:
| Item | Price ($) | Weight (lbs) |
|---|---|---|
| Stereo | 3000 | 4 |
| Laptop | 2000 | 3 |
| Guitar | 1500 | 1 |
DP approach -
We use a table to store results and build the solution step by step. The idea is:
- If an item fits in the remaining weight, we choose between:
- Taking it (adding its value + best previous option).
- Leaving it (keeping the best previous option).
- If it doesn’t fit, we just take the previous best value.
Lets take each row, one by one -
1. Guitar Row
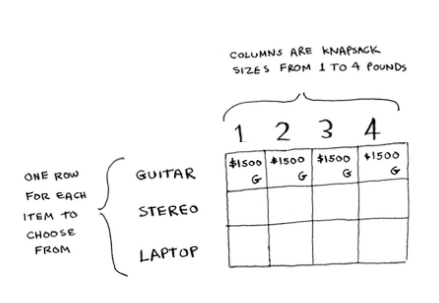
The first cell has a capacity of 1 lb, guitar can fit in it so value of the cell is $1500.
The same for the rest of the cells in this row. Remember, this is the first row, so you have only the guitar to choose from. You’re pretending that the other two items aren’t available to steal right now.
2. Stereo Row
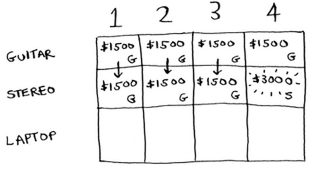
As stereo is 4lb, we take $1500 max till knapsack is at 3lb capacity. At 4lb capacity we have to choose between taking stereo or leaving it. We take it and value is $3000.
3. Laptop Row
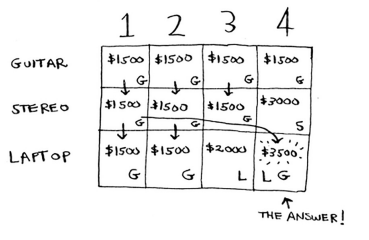
The laptop weighs 3 lb, so it won’t fit into a 1 lb or a 2 lb knapsack. The estimate for the first two cells stays at $1,500.
At 3 lb, the old estimate was $1,500. But you can choose the laptop instead, and that’s worth $2,000.
At 4 lbs capacity, choosing guitar (1 lb) + laptop (3 lb) gives $3500, which is better than just the stereo ($3000), so we update the cell to $3500
The formula at play here was -