Greedy Algorithms

A greedy algorithm is simple: at each step, pick the most optimal move without considering future consequences. While greedy algorithms are efficient, they don’t always produce the best solution.

Example 1: Scheduling Classes

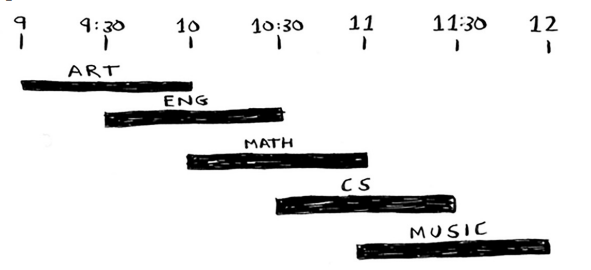
Problem asks us to hold as many classes as possible in this classroom.

A Greedy approach to solve this is -

• Select the class that ends earliest
• Pick next class that starts after previous class ends
• Repeat until no more classes can fit

---

Example 2: Knapsack problem

You have a knapsack that can hold 35 kg. A shop offers the following items:

Item	Price ($)	Weight (kg)
Stereo	3000	30
Laptop	2000	20
Guitar	1500	15

Greedy approach -

• Pick heaviest valuable item first.
• Repeat until sack is full

Note - Check how here Greedy approach fails. If we pick 30KG, we only get $3000, but if we would have picked Laptop(20KG) and Guitar(15KG) - $3500

---

Example 3: The Set Covering Problem

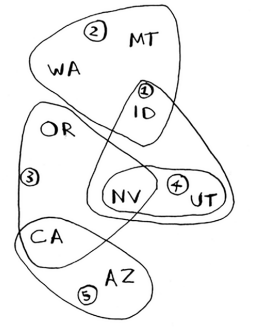
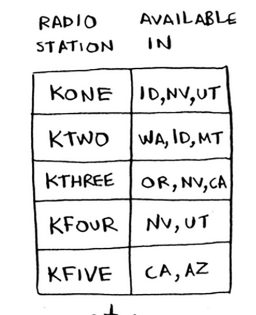
Each station covers a region, and there’s overlap. How do you figure out the smallest set of stations you can play on to cover all 50 states ?

Solution 1: Brute Force -

Generate all possible subsets of stations (2^n combinations). Choose smallest subset that covers all states. Time complexity it’ll take is O(2^n) so too slow for large datasets.

Solution 2: Greedy -

1. Pick the station that covers the most uncovered states.
2. Repeat until all the states are covered

Time complexity - O(n^2)

Implementation -

import java.util.*;

public class StationSelection {

    public static void main(String[] args) {
        Set<String> statesNeeded = new HashSet<>(List.of("mt", "wa", "or", "id", "nv", "ut", "ca", "az"));

        Map<String, Set<String>> stations = Map.of(
                "kone", Set.of("id", "nv", "ut"),
                "ktwo", Set.of("wa", "id", "mt"),
                "kthree", Set.of("or", "nv", "ca"),
                "kfour", Set.of("nv", "ut"),
                "kfive", Set.of("ca", "az")
        );

        Set<String> finalStations = new HashSet<>();

        while (!statesNeeded.isEmpty()) {
            String bestStation = null;
            Set<String> statesCovered = new HashSet<>();

            for (Map.Entry<String, Set<String>> entry : stations.entrySet()) {
                Set<String> covered = new HashSet<>(statesNeeded);
                covered.retainAll(entry.getValue()); // retain only the elements that are common between covered and the set of states covered by the current station

                if (covered.size() > statesCovered.size()) {
                    bestStation = entry.getKey();
                    statesCovered = covered;
                }
            }

            statesNeeded.removeAll(statesCovered);
            finalStations.add(bestStation);
        }

        System.out.println("Final selected stations: " + finalStations);
    }
}