Breadth-First Search

Back to Data Structures and Algorithms
Arjit Sharma
02 Mins

Graphs

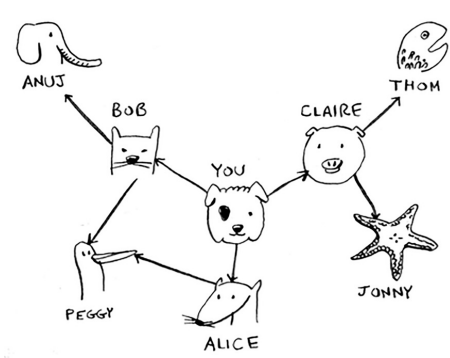
A graph is a data structure made up of nodes (also called vertices) and edges. It is used to model relationships and connections between different entities. Example - Maps and Navigation ( Cities as nodes, Roads as edges )

Breadth-First Search (BFS)

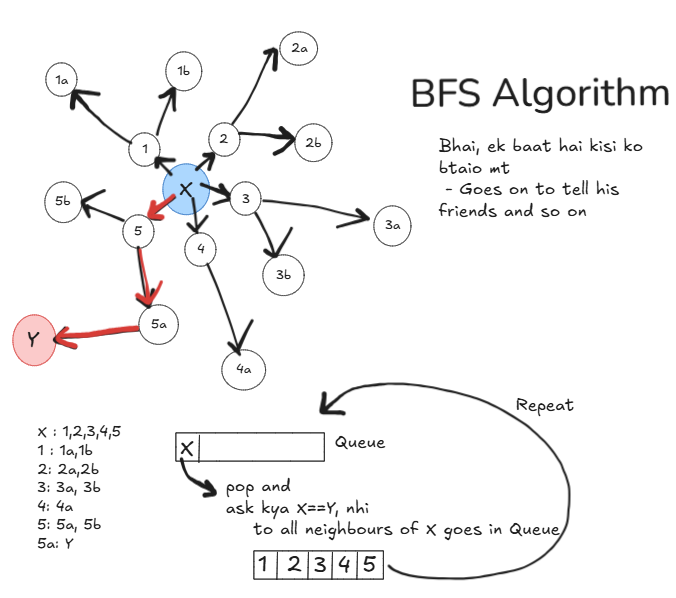
BFS is a graph traversal algorithm that answers two key questions:

  1. Is there a path from Node A to Node B?

    Imagine you are looking for a mango seller in your social network. BFS starts with your immediate friends and checks if any of them are mango sellers. If not, it adds their friends to the search list and continues.

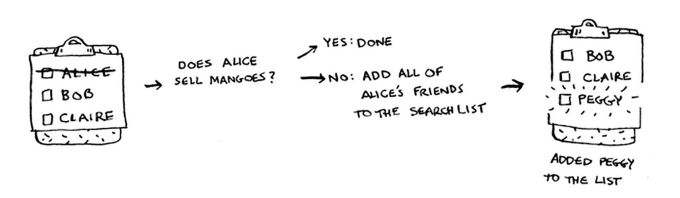
Untitled

Untitled

  1. What is the shortest path from Node A to Node B?

    BFS finds the shortest path in an unweighted graph, meaning it finds the closest mango seller with minimal steps.

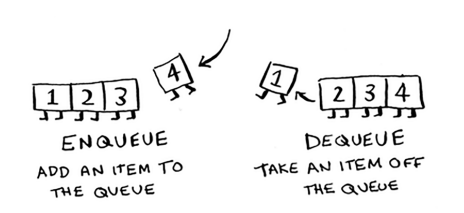
Queues

A queue is like a line at a store. People (or items) join at the back and leave from the front.

Untitled

Implementing a Graph

A hash table (map) can be used to represent a graph, where each node maps to a list of its neighbors.

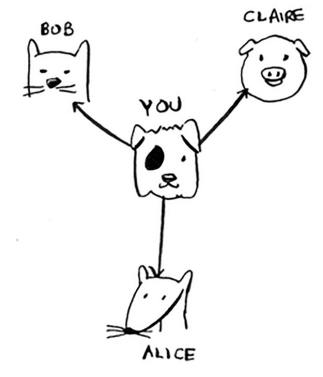
Untitled

Untitled

Map<String, List<String>> graph = new HashMap<>();
graph.put("you", Arrays.asList("alice", "bob", "claire"));

BFS Algorithm Implementation

image.png

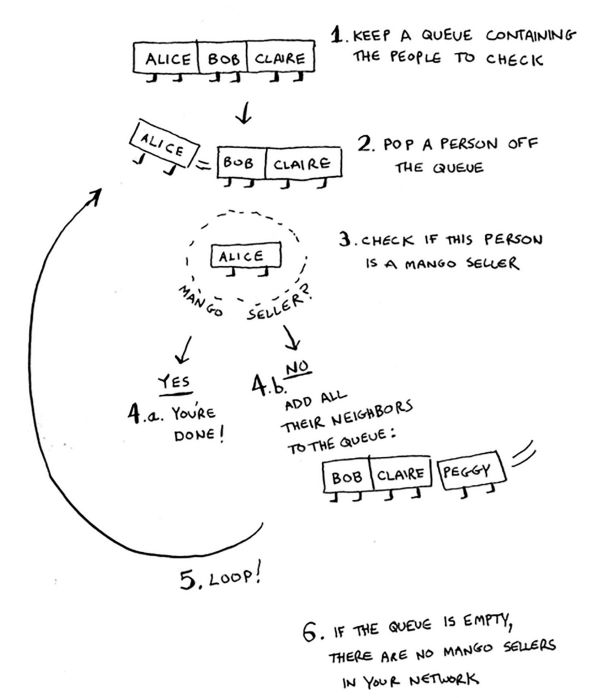
Untitled

public static boolean isMangoSeller(Map<String, List<String>> graph, String startPerson) {
        Queue<String> queue = new LinkedList<>();
        Set<String> visited = new HashSet<>();

        queue.add(startPerson);

        while (!queue.isEmpty()) {
            String person = queue.poll();
            
            // Replace this condition with logic for mango seller
            if (person.endsWith("mango")) {
                System.out.println(person + " is a mango seller!");
                return true;
            }

            // Mark the person as visited to avoid cycles
            visited.add(person);

            // Add unvisited neighbors to the queue
            List<String> neighbors = graph.get(person);
            for (String neighbor : neighbors) {
                if (!visited.contains(neighbor)) {
                    queue.add(neighbor);
                }
            }
        }

        System.out.println("No mango seller found in the network.");
        return false;
    }

The running time of BFS depends on:

  • Adding all vertices to the queue (V)
  • Traversing all edges (E)

Time Complexity: O(V + E)

BFS is efficient for finding shortest paths and ensuring all nodes are visited in the least number of steps.

Next →