Formal Grammars & Chomsky Hierarchy

Back to Automata Theory
Arjit Sharma
02 Mins

What Is a Grammar?

A grammar is a set of rules used to generate strings in a language. It tells you how to build valid sentences (or code) from a set of symbols.

A grammar includes:

  • Start symbol: where generation begins
  • Terminals: actual symbols (like a, b, or +)
  • Non-terminals: placeholders (like or S)
  • Production rules: how symbols can be replaced

Example

S → aSb | ε
  • S is Start Symbol and Non-terminal
  • a and b are Terminals
  • There are 2 production rules (S → aSb and S → ε)

This generates strings like ab, aabb, aaabbb, etc.

Regular vs Non-Regular Grammar

  • A regular grammar produces regular languages, the simplest kind.

    It uses rules like:

    A → aB
B → b

  • A non-regular grammar is more powerful and can describe structures finite automata cannot, like:

    S → aSb | ε

    This generates equal numbers of a’s and b’s, which is valid in context-free grammars.

Chomsky Hierarchy (1956)

Noam Chomsky formalized grammar types into 4 levels -

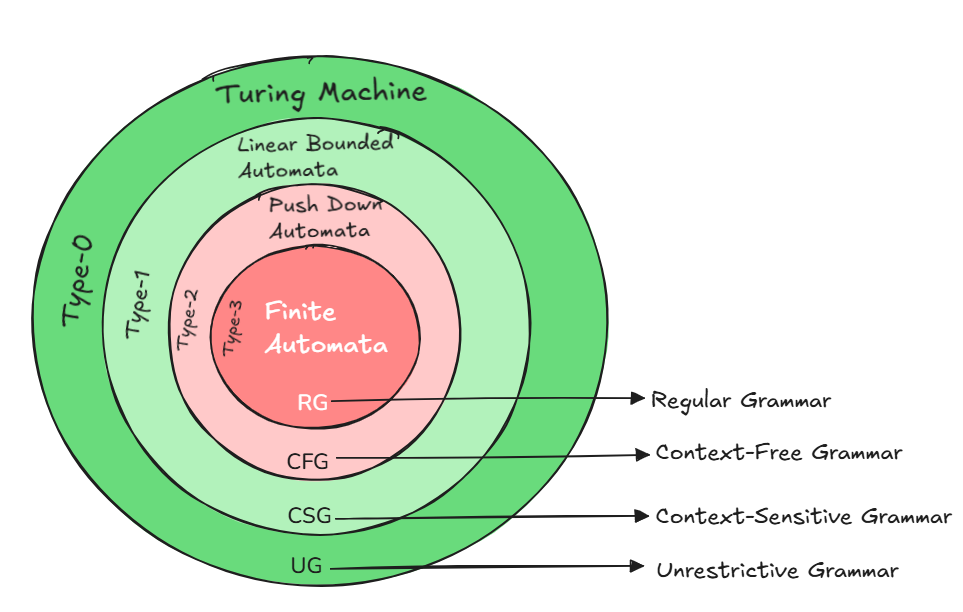
chomsky-hierarchy

TypeGrammar TypeRecognized ByExamples
0UnrestrictedTuring MachineAny computable language
1Context-sensitiveLinear Bounded Automatonaⁿbⁿcⁿ
2Context-freePushdown Automaton (PDA)Balanced parentheses, arithmetic
3RegularFinite AutomatonKeywords, identifiers

Regular languages (Type 3) are the simplest and most limited, but also the fastest to recognize. As you go up the hierarchy, you can express more complex patterns, but need more powerful machines.

Context-Free Grammars (CFGs)

A context-free grammar allows productions of the form:

A → γ

Where A is a single non-terminal, and γ can be any string of terminals and non-terminals.

This allows recursive structures, such as:

  • Arithmetic expressions (Expr → Expr + Term)
  • Balanced parentheses (S → (S) | ε)
  • Nested blocks in code

Example CFG:

S → aSb | ε

Generates: ε, ab, aabb, aaabbb …

Need of CFG ?

Finite automata (and regular grammars) cannot count or remember, so they can’t ensure matching numbers of symbols (like open and close brackets). CFGs solve that with a stack-based memory (via Pushdown Automata).

CFGs are used by parsers in compilers to understand nested syntax.

Conclusion

  • Grammars define how valid strings are built using a set of production rules.
  • Chomsky hierarchy classifies grammars by complexity
  • Context-free grammars can describe structured input, ideal for programming languages
Next →