Boolean Algebra
Boolean algebra is a system of logic developed to manipulate and simplify expressions made up of binary values - true or false, 1 or 0.
Started by George Boole in 1800s with a purpose to create Mathematical framework to describe logic operations. A century later it became the foundation for designing all digital circuits and computers.
Core Operations
These three operations are the building blocks of all digital logic -
- AND (·) - Outputs 1 only if both inputs are 1. Ex - Login requires password AND username
- OR (+) - Outputs 1 if at least one input is 1. Ex - Unlock a phone with Face ID OR PIN
- NOT (¬ or !) - Flips the input. Ex - If door is NOT closed, washing machine stops
Boolean Algebra Laws
| Law Name | Expression(s) | Meaning |
|---|---|---|
| Identity | A + 0 = A A · 1 = A | Adding false or multiplying by true doesn’t change the value |
| Null | A + 1 = 1 A · 0 = 0 | OR with true always gives true; AND with false always gives false |
| Idempotent | A + A = A A · A = A | Repeating a condition has no effect |
| Complement | A + ¬A = 1 A · ¬A = 0 | A condition or its opposite is always true in OR; always false in AND |
| Domination | A + 1 = 1 A · 0 = 0 | Dominating values (1 in OR, 0 in AND) override everything |
| Double Negation | ¬(¬A) = A | Negating a value twice gives back the original value |
| Commutative | A + B = B + A A · B = B · A | Order doesn’t affect outcome for OR and AND |
| Associative | (A + B) + C = A + (B + C) (A · B) · C = A · (B · C) | Grouping doesn’t affect outcome |
| Distributive | A · (B + C) = A·B + A·C A + (B · C) = (A + B) · (A + C) | Distribute one operation over another (like multiplying over addition) |
| Absorption | A + A·B = A A · (A + B) = A | Redundant conditions can be removed |
| De Morgan’s | ¬(A · B) = ¬A + ¬B ¬(A + B) = ¬A · ¬B | Converts AND to OR (and vice versa) when negating entire expressions |
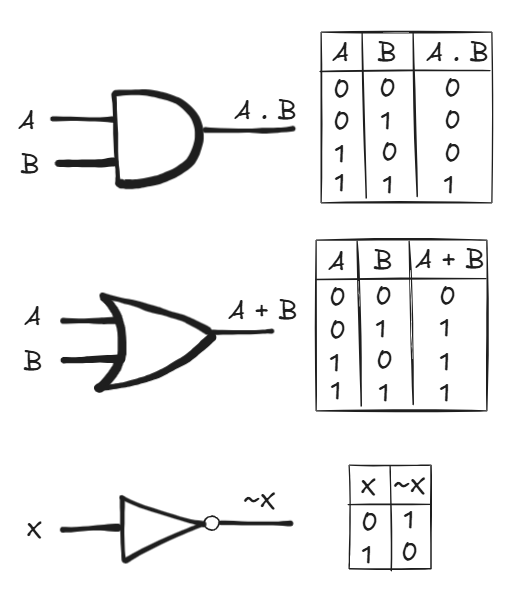
Logic Gates
Boolean operations come to life as logic gates in electronic circuits. These gates are wired together in chips to perform tasks like addition, memory storage etc., forming a backbone for digital electronics.
| Operation | Gate | Behavior |
|---|---|---|
| A · B | AND | 1 only if both A and B are 1 |
| A + B | OR | 1 if A or B is 1 |
| ¬A | NOT | Inverts A (0 → 1, 1 → 0) |
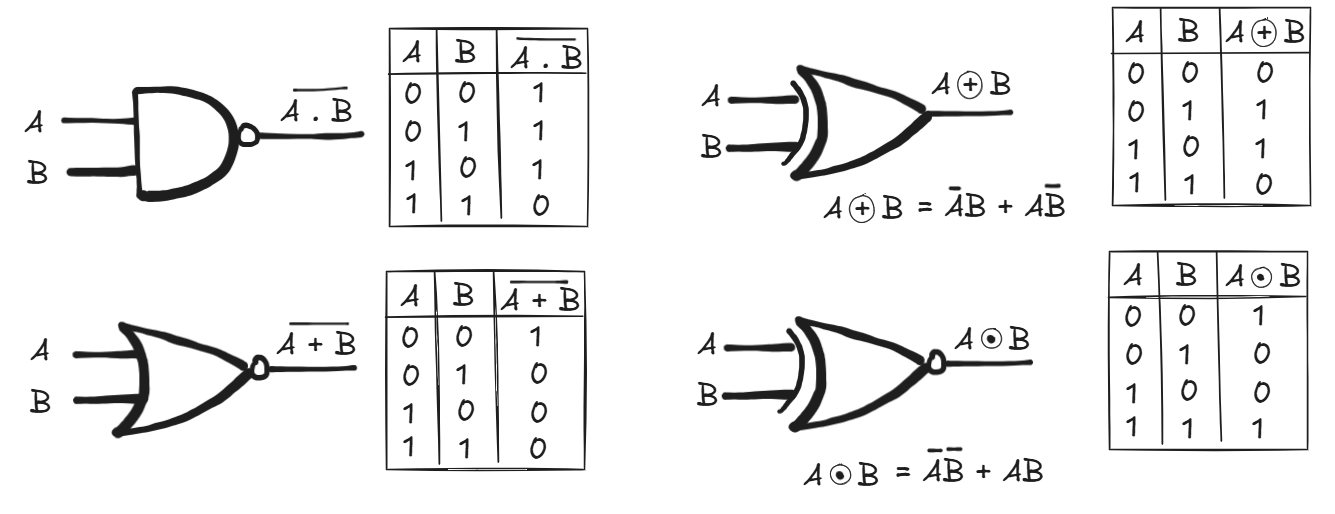
Derived Gates
- NAND: ¬(A · B) - Simply means Not-And.
- NOR: ¬(A + B) - Simply means Not-Or
- XOR: A ⊕ B - Outputs 1 if inputs differ (A or B, but not both).
- XNOR: ¬(A ⊕ B) - Outputs 1 if inputs are the same.
Conclusion
Boolean algebra lets engineers create simple rules that machines can follow. By breaking down decisions into yes/no logic, we make systems more reliable and predictable.