Boolean Expressions

A Boolean expression describes a digital circuit’s behavior using binary variables (0 or 1) and logical operators. It’s like a recipe for how inputs produce an output in a circuit.

Building Blocks

A boolean expression is built of Variable, Operator and Constants.

• Variables: A, B, C, etc. (binary inputs)
• Operators: AND (·) , OR (+) , NOT (¬)
• Constants: 0 (false), 1 (true)

Example: F = A·¬B + C , its read as Output F is 1 if (A AND NOT B) OR C is true

Standard Forms

Boolean expressions are generally written in one of either standard form.

1. Sum of Products (SOP) - OR of AND terms

   Example: F = A·B + ¬A·C

2. Product of Sums (POS) - AND of multiple OR terms

   Example: F = (A + B) · (¬A + C)

These forms are useful for translating expressions directly into gate level circuits.

---

Simplifying Expressions

Simplification helps reduce the number of gates in a circuit. This can be done using -

Boolean Algebra

Use boolean algebra rules to simplify expression.

Example - F = A·B + A·¬B

On applying Boolean identity: F = A(B + ¬B)

Since B + ¬B = 1, we get F = A·1 = A

This tells us the logic only depends on A and B is irrelevant.

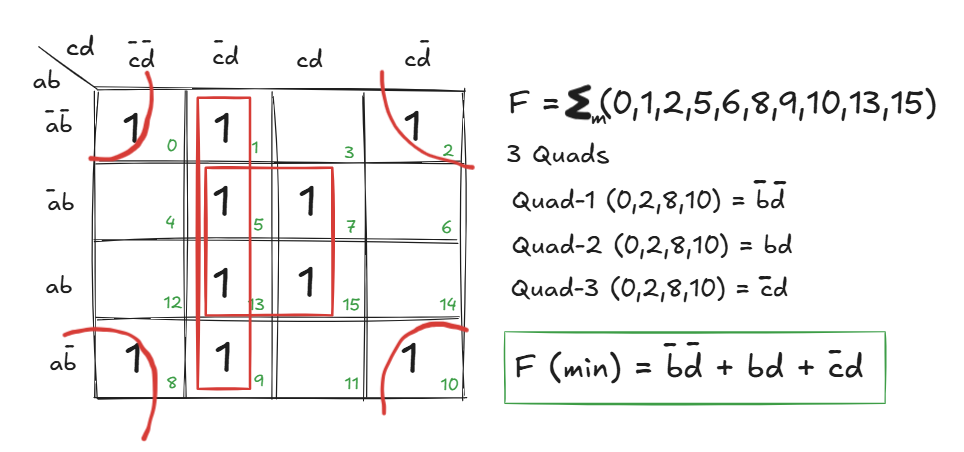
Karnaugh Maps (K-maps)

A K-map is a grid-based tool to simplify Boolean expressions (best for 2-4 variables).

Steps:

1. Fill in 1s for where the output is true.
2. Group adjacent 1s in pairs, quads or octets
3. Derive a simplified term for each group (combine variables that stay constant)