Boolean Algebra
Boolean algebra is the math behind digital electronics, using just two values: 0 (false) and 1 (true). It’s the foundation for designing all digital circuits and computers.
Core Operations
These three operations are the building blocks of all digital logic -
- AND (·) - Outputs 1 only if both inputs are 1.
- OR (+) - Outputs 1 if at least one input is 1.
- NOT (¬ or !) - Flips the input.
Key Rules for Simplification
Boolean algebra uses rules to simplify complex logic, making circuits efficient
- Identity: A + 0 = A, A · 1 = A
- Null: A + 1 = 1, A · 0 = 0
- Idempotent: A + A = A, A · A = A
- Complement: A + ¬A = 1, A · ¬A = 0
- Distributive:
- A · (B + C) = A·B + A·C
- A + (B · C) = (A + B) · (A + C)
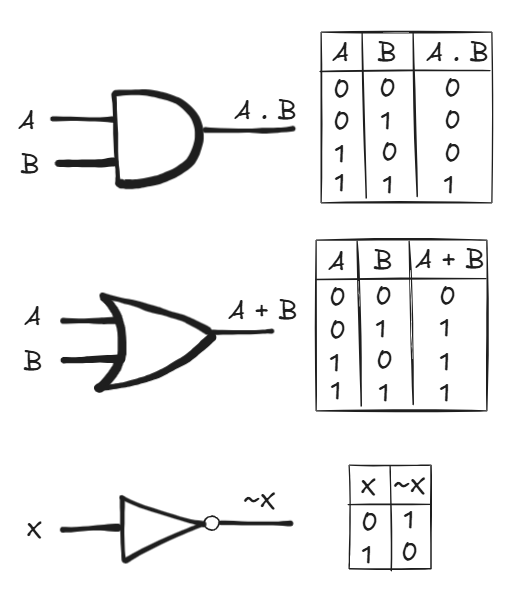
Logic Gates
Boolean operations come to life as logic gates in electronic circuits. These gates are wired together in chips to perform tasks like addition, memory storage etc., forming a backbone for digital electronics.
| Operation | Gate | Behavior |
|---|---|---|
| A · B | AND | 1 only if both A and B are 1 |
| A + B | OR | 1 if A or B is 1 |
| ¬A | NOT | Inverts A (0 → 1, 1 → 0) |
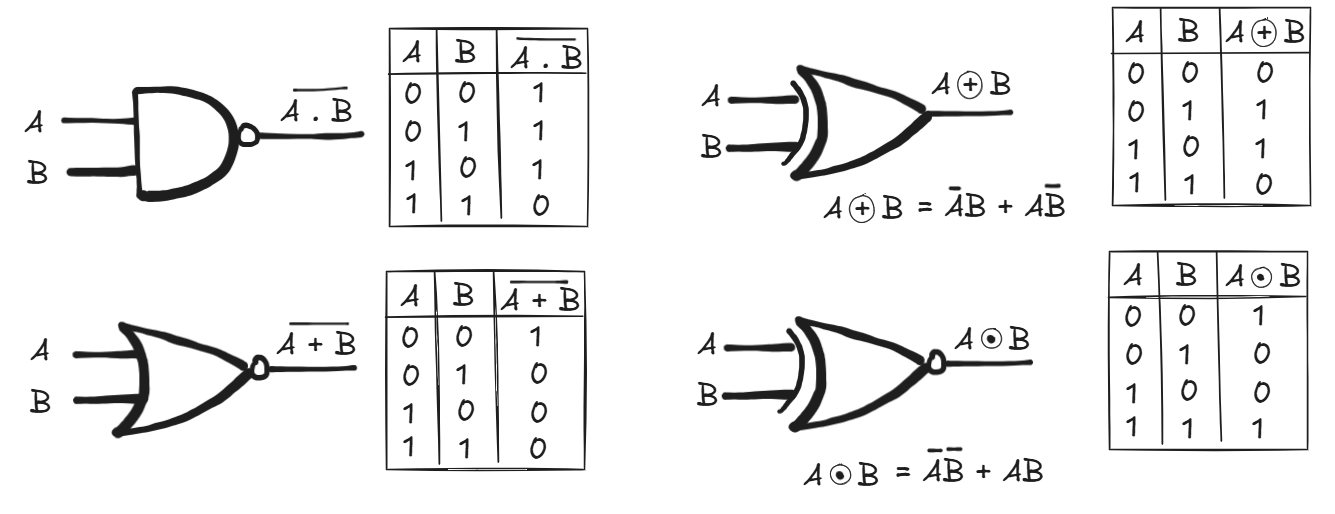
Derived Gates
- NAND: ¬(A · B)
- NOR: ¬(A + B)
- XOR: A ⊕ B - Outputs 1 if inputs differ (A or B, but not both).
- XNOR: ¬(A ⊕ B) - Outputs 1 if inputs are the same.