Functions

Back to Discrete Mathematics
Arjit Sharma
01 Min

What is a Function ?

In math and code, a function is a rule that assigns exactly one output to each input. In discrete math, it is a relation between sets that associates every element for first set to exactly one element of second set.

A function f  from set A to set B:

f: A → B

means every element in A is paired with one and only one element in B. Usage example can be in a website where email is mapped to a user account.

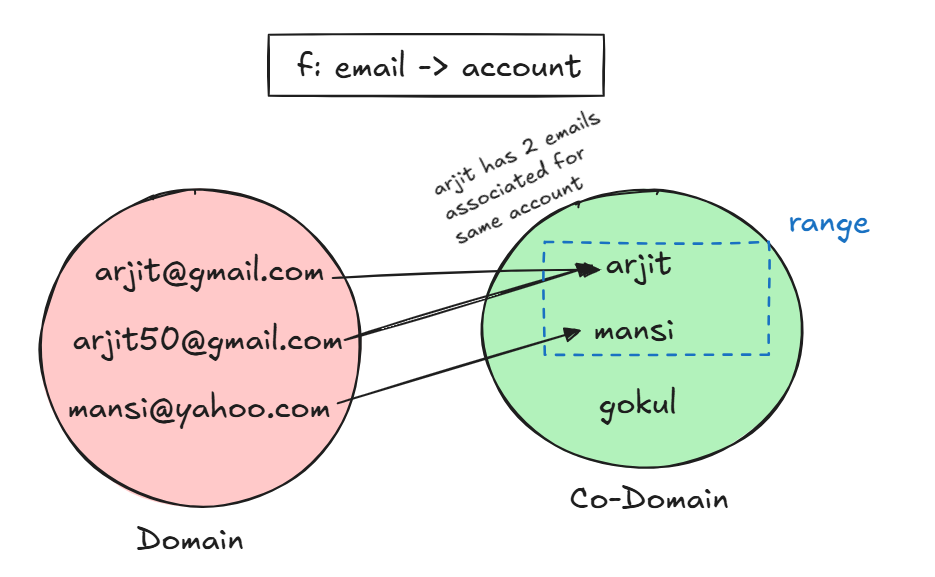
function

Function Composition

Function composition (f . g)(x) means applying function g first, then applying f to the result: f(g(x))

const trim = str => str.trim();
const toLowerCase = str => str.toLowerCase();

// Composed function
const cleanEmail = str => toLowerCase(trim(str));

// Usage
cleanEmail("  arjit@Gmail.COM   ")

Types of Functions

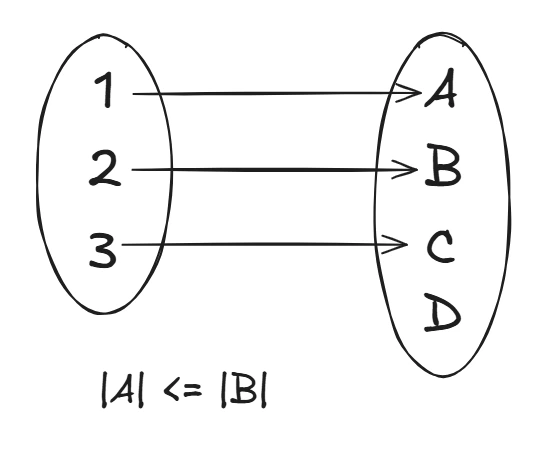
1. Injective (One-to-One)

Each input maps to a unique output. No two users share the same email.

injective

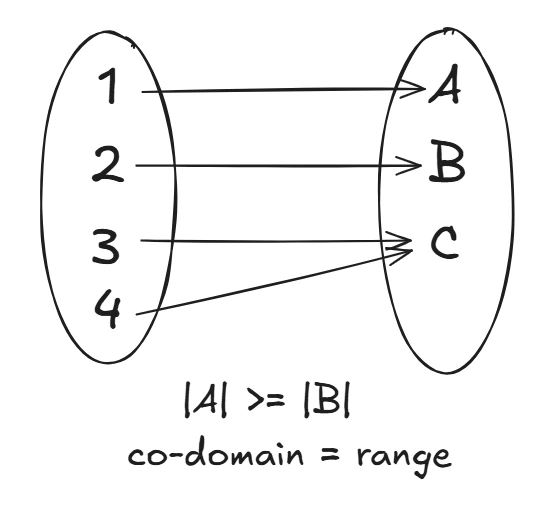
2. Surjective (Onto)

Every output is used at least once. Every department in a company must have atleast one employee.

surjective

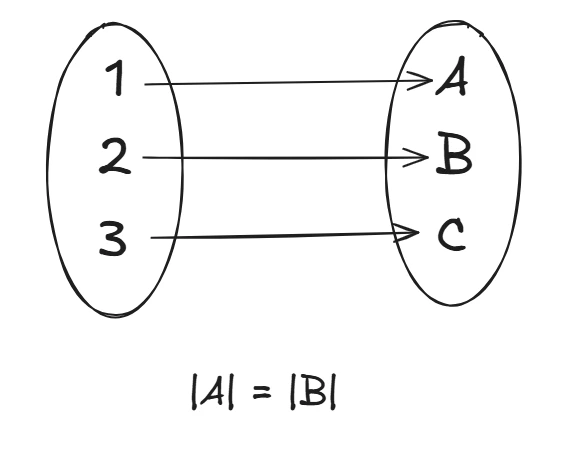
3. Bijective (One-to-One & Onto)

Perfect pairing where each input has exactly one output and vice versa. Each country has only 1 currency associated to it.

bijective

Inverse of a Function

To find the inverse of a function, you essentially “undo” its operation. That means if a function maps f(x) = y, the inverse function will reverse this mapping and is represented as f⁻¹(x). Inverses have powerful applications in fields like encryption, computer graphics, data modeling, and more.

Example - Let f(x)=5x-7, to find the inverse ->

Set y = 5x-7 and solve for x; 
5x-7 = y 
5x = y+7 
x = (y+7)/5

f⁻¹(x)=(x+7)/5

Conclusion

Functions aren’t just pieces of code, they’re structured relationships with properties. Understanding those properties helps when building logic that’s traceable, invertible, and robust.

Next →