POSETs & Lattices

Back to Discrete Mathematics
Arjit Sharma
02 Mins

A Partially Ordered Set (POSET), is just a set where some elements have a clear order, and others don’t need to. It is a Set based on Partial Order Relation.

What’s a POSET?

It follows properties of partial order relation.

  • Reflexive: Every element is related to itself
  • Antisymmetric: If A ⊆ B and B ⊆ A, then A = B
  • Transitive: If A ⊆ B and B ⊆ C, then A ⊆ C

This isn’t a total order, not everything has to be comparable.

Visualizing with a Hasse Diagram

A POSET is often visualized with a Hasse diagram**,** a graph where nodes (items) and edges(direct relationships without showing every indirect link) exists.

Example: A set {1,2,4,8} , where aRb means “a divides b”

Its POSET will be {(1,1), (1,2), (1,4), (1,8), (2,2), (2,4), (2,8), (4,4), (4,8), (8,8)}

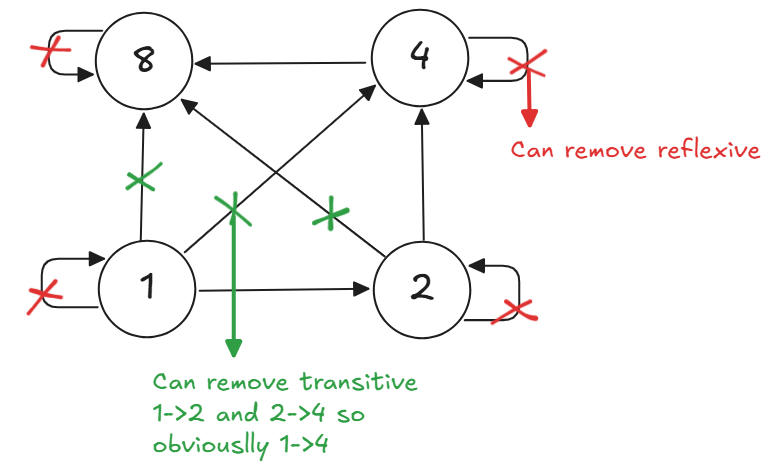
Hasse-Diagram

Hasse Diagram will be →

  8
  |
  4
  |
  2
  |
  1

1 divides {1,2,4,8}. 2 divides {2,4,8} and so on. Now we have a simple way to represent a POSET.

Importance of POSETs

In previous article, we saw importance of partial order relations. Some common examples of POSETs usage are Version trees, Project management tools(Trello, Asana), dependency chains and many more. They’re also a base for topological sorting, which many build tools and task schedulers rely on.

Lattices

A lattice is a partially ordered set where every pair of elements has both a unique smallest upper bound (join) and a unique greatest lower bound (meet).

Example - Consider the set of all divisors of 12: {1, 2, 3, 4, 6, 12}

           12
         /  |  \
        6   4   3
        |   |   |
        2   2   3
         \  |  /
           1

In above Hasse diagram you can check for every pair their exists a Join and a Meet. In this case representing LCM if a Join and GCD if a Meet.

This is basically structured merging and comparison and it’s everywhere in systems design.

Conclusion

POSETs help you reason about “what needs to happen before what” without forcing strict order where it’s unnecessary. They keep systems flexible, efficient, and accurate.

Lattices bring structure to chaos. When your system needs to merge, compare, or combine things predictably, lattices are likely hiding underneath.

Next →